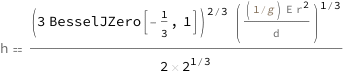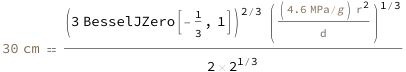Maximum Stable Sand Castle Height
A sand castle is a type of sand sculpture resembling a miniature building. Its height depends on a number of factors, such as the shape, size and mixture of the sand grains, the moisture content and the details of the structure itself.
The maximum height is proportional to the cubic root of the product of the elastic modulus of the sand and the base radius squared divided by the density.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 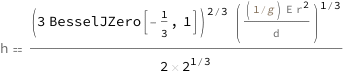 |
Use some values:
| Out[3]= | 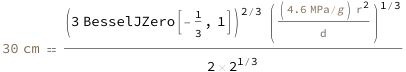 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["h", "Height"] == ((3*BesselJZero[-1/3, 1])^(2/3)*((Quantity[1, "StandardAccelerationOfGravity"^(-1)]*QuantityVariable["E", "ElasticModulus"]*QuantityVariable["r", "Radius"]^2)/QuantityVariable["d", "MassDensity"])^(1/3))/(2*2^(1/3))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/753/753e5c20-f3db-45c1-b42d-9fdbcf28686d/Webpage/FormulaImage.png)