Equation of Circular Motion under Constant Acceleration
The equation of circular motion describes an object moving under constant angular acceleration in a circular as a function of time.
The final position for ciruclar motion equals the intial angle plus the initial angular velocity times the time plus half the angular acceleration times the time squared.
Formula
![Copy to Clipboard QuantityVariable[Subscript["θ", "f"], "Angle"] == (QuantityVariable["t", "Time"]^2*QuantityVariable["α", "AngularAcceleration"])/2 + QuantityVariable[Subscript["θ", "i"], "Angle"] + QuantityVariable["t", "Time"]*QuantityVariable[Subscript["ω", "i"], "AngularVelocity"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/71c/71cb3143-c278-4524-ab97-fe3115a16216/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| θf | final angle | "Angle" |
| t | time | "Time" |
| α | angular acceleration | "AngularAcceleration" |
| θi | initial angle | "Angle" |
| ωi | initial angular velocity | "AngularVelocity" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Equation of Circular Motion under Constant Acceleration"], \
{QuantityVariable[
\!\(\*SubscriptBox[\("\[Theta]"\), \("i"\)]\),"Angle"] ->
Quantity[0, "Radians"],
QuantityVariable["\[Alpha]","AngularAcceleration"] ->
Quantity[1, ("Radians")/("Seconds")^2],
QuantityVariable["t","Time"] -> Quantity[1, "Seconds"]}]](images/71c/71cb3143-c278-4524-ab97-fe3115a16216-io-3-i.en.gif) |
| Out[3]= | 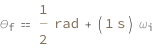 |