Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Sample Size for Estimating a Binomial Parameter

The sample size for estimaitng a binomial parameter estimates the minimum sample size to estimate the binomial parameter.

The sample size equals twice the product of the inverse error function of the confidence level, 1 minus the sample proportion and the sample proportion divided by the margin of error squared.

Formula

QuantityVariable["n", "Unitless"] == (2*InverseErf[QuantityVariable["c", "Unitless"]]^2*(1 - QuantityVariable[OverHat["p"], "Unitless"])*QuantityVariable[OverHat["p"], "Unitless"])/QuantityVariable["M", "Unitless"]^2

symbol description physical quantity
n sample size "Unitless"
c confidence level "Unitless"
M margin of error "Unitless"
pHat sample proportion "Unitless"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Sample Size for Estimating a Binomial Parameter"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ ResourceObject["Sample Size for Estimating a Binomial Parameter"]]
Out[2]=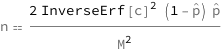

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Sample Size for Estimating a Binomial Parameter"], \ {QuantityVariable["c","Unitless"] -> 0.95`, QuantityVariable["M","Unitless"] -> 0.1`, QuantityVariable[ \!\(\*OverscriptBox[\("p"\), \(^\)]\),"Unitless"] -> 0.5`}]
Out[3]=

Publisher Information