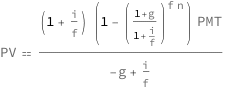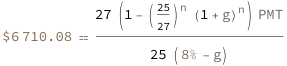Present Value of Annuity Due
An annuity is a series of payments made at equal intervals. An annuity due is an annuity whose payments are made at the beginning of each period. The present value of an annuity is the value of a stream of payments, discounted by the interest rate to account for the fact that payments are being made at various moments in the future.
The present value of an annuity due depends on the value of periodic payments multiplied by the discounted interest compounded over the number of payments, accounting for the frequency of payments and any growth in the periodic payments.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 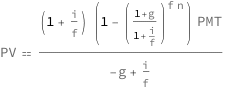 |
Use some values:
| Out[3]= | 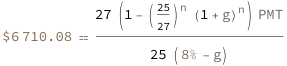 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["PV", "Money"] == ((1 + QuantityVariable["i", "Unitless"]/QuantityVariable["f", "Unitless"])*(1 - ((1 + QuantityVariable["g", "Unitless"])/(1 + QuantityVariable["i", "Unitless"]/QuantityVariable["f", "Unitless"]))^(QuantityVariable["f", "Unitless"]*QuantityVariable["n", "Unitless"]))*QuantityVariable["PMT", "Money"])/(-QuantityVariable["g", "Unitless"] + QuantityVariable["i", "Unitless"]/QuantityVariable["f", "Unitless"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/6e2/6e2f859d-8b1e-4ebe-8206-e254bdb6dea2/Webpage/FormulaImage.png)