Colebrook–White Equation for Darcy–Weisbach Friction Factor
The Colebrook–White equation expresses the Darcy friction factor as a function of the Reynolds number and pipe relative roughness, fitting the data of experimental studies of turbulent flow in smooth and rough pipes.
The Colebrook-White equation relates the relative pipe roughness, Reynolds number and Darcy-Weisbach friction factor through a series of logarithms.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= |  |
Use some values:
| Out[3]= | 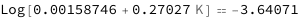 |
External Links
Publisher Information
![Copy to Clipboard 1/Sqrt[QuantityVariable["λ", "DarcyWeisbachFrictionFactor"]] == (-2*Log[0.27027027027027023*QuantityVariable["K", "Unitless"] + 2.51/(QuantityVariable["Re", "ReynoldsNumber"]*Sqrt[QuantityVariable["λ", "DarcyWeisbachFrictionFactor"]])])/Log[10]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/6b3/6b3a5f14-a16e-41f8-bd67-042d153adb66/Webpage/FormulaImage.png)