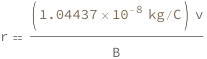Circular Orbit Radius of a Charged Particle in a Magnetic Field
A charged particle moving in a magnetic field will be pushed into a circular path by the interaction of the charge and the magnetic field. The radius of that path can be calculated from the properties of the charge and the magnetic induction.
The radius of the circular orbit of a charged particle in a magnetic field equals the product of the mass and speed of the particle divided by the particle charge and the magnetic induction.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 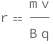 |
Use some values:
| Out[3]= | 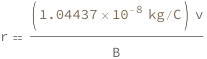 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["r", "Radius"] == (QuantityVariable["m", "Mass"]*QuantityVariable["v", "Speed"])/(QuantityVariable["B", "MagneticInduction"]*QuantityVariable["q", "ElectricCharge"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/6a1/6a1508be-09d5-4e87-a6ea-f8e4b4be1dfe/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Circular Orbit Radius of a Charged Particle in a Magnetic Field"], \
{QuantityVariable["q","ElectricCharge"] ->
Quantity[1.6000000000000002`*^-19, "Coulombs"],
QuantityVariable["m","Mass"] -> Quantity[1.671`*^-27, "Kilograms"]}]](images/6a1/6a1508be-09d5-4e87-a6ea-f8e4b4be1dfe-io-3-i.en.gif)