Moment of Inertia of a Sphere
The mass moment of inertia measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analogue to mass. For a uniform solid sphere, the moments of inertia are taken to be about an axis passing through the sphere's center of mass.
The moment of inertia of a uniform solid sphere is proportional to the mass and the square of the radius.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 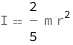 |
Use some values:
| Out[3]= | 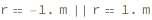 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["I", "MomentOfInertia"] == (2*QuantityVariable["m", "Mass"]*QuantityVariable["r", "Radius"]^2)/5](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/68b/68b9fd46-7767-4173-8e58-9270df6e7002/Webpage/FormulaImage.png)
