Prism Refraction
A prism is a transparent optical element with flat, polished surfaces that refract light. At least two of the flat surfaces must have an angle between them, called the apex angle.
The angle of deviation equals the sum of the angle of incidence and the angle of transmission minus the apex angle. The sine of the angle of transmission equals the difference between the product of the sine of the apex angle and the square root of the refractive index squared minus the sine squared of the angle of incidence and the cosine of the apex angle times the sine of the angle of incidence.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 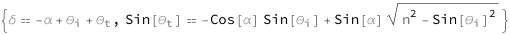 |
Use some values:
| Out[3]= | 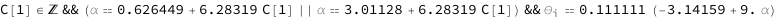 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["δ", "Angle"] == -QuantityVariable["α", "Angle"] + QuantityVariable[Subscript["θ", "i"], "Angle"] + QuantityVariable[Subscript["θ", "t"], "Angle"], Sin[QuantityVariable[Subscript["θ", "t"], "Angle"]] == -(Cos[QuantityVariable["α", "Angle"]]*Sin[QuantityVariable[Subscript["θ", "i"], "Angle"]]) + Sin[QuantityVariable["α", "Angle"]]*Sqrt[QuantityVariable["n", "RefractiveIndex"]^2 - Sin[QuantityVariable[Subscript["θ", "i"], "Angle"]]^2]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/666/666ff1d7-fd45-45f2-99b0-cb1cd31ee0be/Webpage/FormulaImage.png)
