Equation of Motion Using Angular Displacement
Equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time.
The final angular velocity squared equals the initial angular velocity squared plus twice the angular acceleration times the angular displacement.
Formula
![Copy to Clipboard QuantityVariable[Subscript["ω", "f"], "AngularVelocity"]^2 == 2*QuantityVariable["α", "AngularAcceleration"]*QuantityVariable["θ", "Angle"] + QuantityVariable[Subscript["ω", "i"], "AngularVelocity"]^2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/666/6667650d-3443-4d9c-aed8-2931862444db/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| ωf | final angular velocity | "AngularVelocity" |
| α | angular acceleration | "AngularAcceleration" |
| θ | angular displacement | "Angle" |
| ωi | initial angular velocity | "AngularVelocity" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |
Use some values:
| In[3]:= |
| Out[3]= | 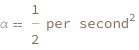 |