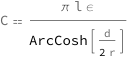Capacitance between Two Parallel Cylinders
A capacitor is a passive, two-terminal electrical component that stores electrical energy in an electric field. In the case of two parallel cylinders, the capacitance builds up between two parallel cylinders of the same radius.
The capacitance is proportional to the product of the length and the permittivity of the insulator between the cylinders divided by the arccosine of the ratio of the distance between the cylinders to twice their radii.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 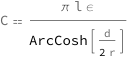 |
Use some values:
| Out[3]= | 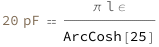 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["C", "ElectricCapacitance"] == (Pi*QuantityVariable["l", "Length"]*QuantityVariable["ε", "ElectricPermittivity"])/ArcCosh[QuantityVariable["d", "Distance"]/(2*QuantityVariable["r", "Radius"])]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/665/665b0b7b-c870-4b3c-a087-6f2aad5c6444/Webpage/FormulaImage.png)