Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

pKa Using Concentrations

An acid dissociation constant is a quantitative measure of the strength of an acid in solution. pKa refers to the logarithm of the acid dissociation constant.

The log acidity constant equals the negative of the base 10 logarithm of the product of the conjugate base concentration and the hydrogen ion concentration divided by the acid concentration.

Formula

QuantityVariable[Subscript["pK", "a"], "Unitless"] == -(Log[(Quantity[1, "Liters"/"Moles"]*QuantityVariable[Row[{"[", Superscript["A", "-"], "]"}], "Molarity"]*QuantityVariable[Row[{"[", Superscript["H", "+"], "]"}], "Molarity"])/QuantityVariable["[HA]", "Molarity"]]/Log[10])

symbol description physical quantity
pKa log acidity constant "Unitless"
[HA] acid concentration "Molarity"
[A-] conjugate base concentration "Molarity"
[H+] hydrogen ion concentration "Molarity"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["pKa Using Concentrations"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["pKa Using Concentrations"]]
Out[2]=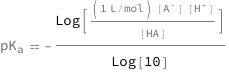

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "pKa Using Concentrations"], {QuantityVariable[ Row[{"[", Row[{"H", "+"}], "]"}],"Molarity"] -> Quantity[0.00042`, ("Moles")/("Liters")], QuantityVariable[ \!\(\*SubscriptBox[\("pK"\), \("a"\)]\),"Unitless"] -> 3.85`, QuantityVariable[Row[{"[", Row[{"A", "-"}], "]"}],"Molarity"] -> Quantity[0.25`, ("Moles")/("Liters")]}]
Out[3]=

Publisher Information