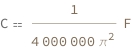Resonance Frequency Equation
An LC circuit, also called a resonant circuit, is an electric circuit consisting of an inductor and a capacitor connected together. The circuit can act as an electrical resonator (an electrical analog of a tuning fork) storing energy oscillating at the circuit's resonant frequency.
The resonance frequency equals the reciprocal of 2\[Pi] times the square root of the electric capacitance times the magnetic inductance.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 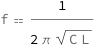 |
Use some values:
| Out[3]= | 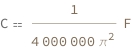 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["f", "Frequency"] == 1/(2*Pi*Sqrt[QuantityVariable["C", "ElectricCapacitance"]*QuantityVariable["L", "MagneticInductance"]])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/62b/62b3aa48-bf1d-4c30-867b-bf4061f41e63/Webpage/FormulaImage.png)