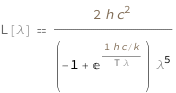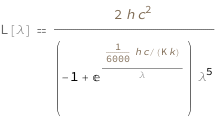Planck's Radiation Law Using Wavelength
Planck's law describes the spectral density of electromagnetic radiation emitted by a blackbody in thermal equilibrium at a given temperature.
The spectral radiance as a function of wavelength is proportional to the reciprocal of the wavelength cubed times the sum of negative 1 and the exponential of the product of the speed of light and the Planck constant divided by the product of the temperature, wavelength and the Boltzmann constant.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 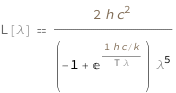 |
Use some values:
| Out[3]= | 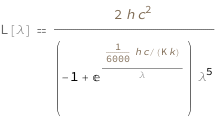 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["L"["λ"], "SpectralRadianceWRTWavelength"] == Quantity[2, "PlanckConstant"*"SpeedOfLight"^2]/((-1 + E^(Quantity[1, ("PlanckConstant"*"SpeedOfLight")/"BoltzmannConstant"]/(QuantityVariable["T", "Temperature"]*QuantityVariable["λ", "Wavelength"])))*QuantityVariable["λ", "Wavelength"]^5)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/629/62996c1b-8530-4759-a67c-416256d8e079/Webpage/FormulaImage.png)