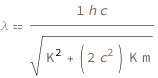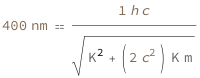Relativistic de Broglie Wavelength by Kinetic Energy
The de Broglie wavelength is the wavelength associated with a massive particle in motion according to quantum mechanics, accounting for relativistic effects.
The de Broglie wavelength is proportional to the reciprocal of the square root of the kinetic energy squares plus the product of the kinetic energy, the mass and twice the square of the speed of light.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 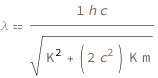 |
Use some values:
| Out[3]= | 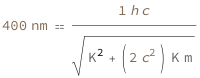 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["λ", "Wavelength"] == Quantity[1, "PlanckConstant"*"SpeedOfLight"]/Sqrt[QuantityVariable["K", "Energy"]^2 + Quantity[2, "SpeedOfLight"^2]*QuantityVariable["K", "Energy"]*QuantityVariable["m", "Mass"]]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/623/623d5f40-6cc0-4f37-8407-d33ecafe21de/Webpage/FormulaImage.png)