Two Infinitely Long Parallel Wires
Currents passing through two infinitely long parallel wires create a magnetic force between the two.
The force on a segment of two infinitely long parallel wires is proportional to the product of the length of the segment and the electrical currents in the wires divided by the distance between them.
Formula
![Copy to Clipboard QuantityVariable["ΔF", "Force"] == (Quantity[1/(2*Pi), "MagneticConstant"]*QuantityVariable["ΔL", "Length"]*QuantityVariable[Subscript["I", "1"], "ElectricCurrent"]*QuantityVariable[Subscript["I", "2"], "ElectricCurrent"])/QuantityVariable["d", "Distance"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/5ef/5ef8699e-6a93-4094-a208-8163e9ed253c/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| ΔF | force on a segment | "Force" |
| d | distance | "Distance" |
| ΔL | length of a segment | "Length" |
| I1 | electrical current 1 | "ElectricCurrent" |
| I2 | electrical current 2 | "ElectricCurrent" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 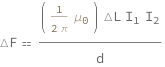 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Two Infinitely Long Parallel Wires"], {QuantityVariable[
"\[CapitalDelta]\[InvisibleSpace]F","Force"] ->
Quantity[2.`*^-7, "Newtons"],
QuantityVariable["\[CapitalDelta]\[InvisibleSpace]L","Length"] ->
Quantity[1, "Meters"], QuantityVariable[
\!\(\*SubscriptBox[\("I"\), \("2"\)]\),"ElectricCurrent"] ->
Quantity[1, "Amperes"]}]](images/5ef/5ef8699e-6a93-4094-a208-8163e9ed253c-io-3-i.en.gif) |
| Out[3]= | 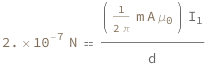 |