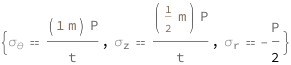Mechanical Stresses on a Thin-Walled Hoop
A cylinder stress is a stress distribution with rotational symmetry, one that remains unchanged if the stressed object is rotated about some fixed axis.
Hoop stress equals pressure times the inner radius divided by the wall thickness. The axial stress equals the pressure times the inner radius divided by twice the wall thickness. Radial stress equals the negative of half the pressure.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 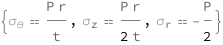 |
Use some values:
| Out[3]= | 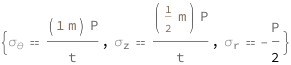 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["σ", "θ"], "Stress"] == (QuantityVariable["P", "Pressure"]*QuantityVariable["r", "Length"])/QuantityVariable["t", "Length"], QuantityVariable[Subscript["σ", "z"], "Stress"] == (QuantityVariable["P", "Pressure"]*QuantityVariable["r", "Length"])/(2*QuantityVariable["t", "Length"]), QuantityVariable[Subscript["σ", "r"], "Stress"] == -QuantityVariable["P", "Pressure"]/2}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/5d2/5d205a61-b613-4939-a944-7e182c77fbdf/Webpage/FormulaImage.png)