Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

First Cowling Number

The Cowling number expresses the magnetic-to-inertia forces ratio.

The first Cowling number equals the product of the magnetic flux density squared, characteristic length and electric conductivity divided by the product of the mass density and the characteristic speed.

Formula

QuantityVariable[Subscript["Co", "1"], "CowlingNumber1"] == (QuantityVariable["B", "MagneticFluxDensity"]^2*QuantityVariable["l", "Length"]*QuantityVariable["σ", "ElectricConductivity"])/(QuantityVariable["v", "Speed"]*QuantityVariable["ρ", "MassDensity"])

symbol description physical quantity
Co1 first Cowling number "CowlingNumber1"
B magnetic flux density "MagneticFluxDensity"
l characteristic length "Length"
v characteristic speed "Speed"
ρ mass density "MassDensity"
σ electric conductivity "ElectricConductivity"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["First Cowling Number"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["First Cowling Number"]]
Out[2]=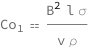

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "First Cowling Number"], {QuantityVariable[ "B","MagneticFluxDensity"] -> Quantity[1, "Milliteslas"], QuantityVariable["\[Sigma]","ElectricConductivity"] -> Quantity[1, ("Siemens")/("Meters")], QuantityVariable["\[Rho]","MassDensity"] -> Quantity[1000, ("Kilograms")/("Meters")^3], QuantityVariable["v","Speed"] -> Quantity[1, ("Meters")/("Seconds")], QuantityVariable["l","Length"] -> Quantity[1, "Meters"]}]
Out[3]=

Source Metadata

  • Creator:

Publisher Information