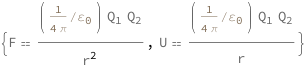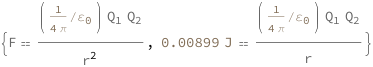Coulomb's Law
The magnitude of the electrostatic force of attraction between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them. The force is along the straight line joining them. If the two charges have the same sign, the electrostatic force between them is repulsive; if they have different signs, the force between them is attractive.
Coulomb's law states that the force is proportional to the product of the charges divided by the radius squared. The potential energy is proportional to the product of the charges divided by the radius.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 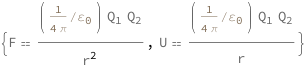 |
Use some values:
| Out[3]= | 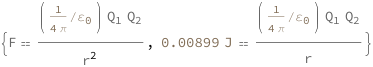 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["F", "Force"] == (Quantity[1/(4*Pi), "ElectricConstant"^(-1)]*QuantityVariable[Subscript["Q", "1"], "ElectricCharge"]*QuantityVariable[Subscript["Q", "2"], "ElectricCharge"])/QuantityVariable["r", "Distance"]^2, QuantityVariable["U", "Energy"] == (Quantity[1/(4*Pi), "ElectricConstant"^(-1)]*QuantityVariable[Subscript["Q", "1"], "ElectricCharge"]*QuantityVariable[Subscript["Q", "2"], "ElectricCharge"])/QuantityVariable["r", "Distance"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/59a/59a5d188-e122-474d-b994-464fada804ce/Webpage/FormulaImage.png)