Mohr's Circle Plane Shear Stress
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. Stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other.
The shear stress in a new frame increases with the shear stress and normal stress in the x and y directions (though a larger normal stress in the y direction will increase it more). The angle of the stress also modifies it.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 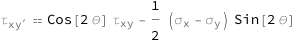 |
Use some values:
| Out[3]= | 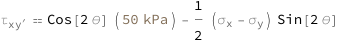 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["τ", Superscript["xy", "′"]], "Stress"] == Cos[2*QuantityVariable["θ", "Angle"]]*QuantityVariable[Subscript["τ", "xy"], "Stress"] - ((QuantityVariable[Subscript["σ", "x"], "Stress"] - QuantityVariable[Subscript["σ", "y"], "Stress"])*Sin[2*QuantityVariable["θ", "Angle"]])/2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/586/586c9098-0932-4dfb-938f-2d19f5904912/Webpage/FormulaImage.png)
