Bose–Einstein Condensation Temperature for Noninteracting Bosons Using Number Density
The Bose–Einstein condensation temperature is the temperature at which a free Bose gas transitions to a Bose–Einstein condensate. Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which point macroscopic quantum phenomena become apparent.
The Bose-Einstein condensation temperature increases as the square of the cubic root of the boson number density increases, and increases inversely with the mass of each boson.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 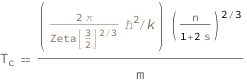 |
Use some values:
| Out[3]= | 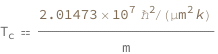 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["T", "c"], "Temperature"] == (Quantity[(2*Pi)/Zeta[3/2]^(2/3), "ReducedPlanckConstant"^2/"BoltzmannConstant"]*(QuantityVariable["n", "InverseVolume"]/(1 + 2*QuantityVariable["s", "Unitless"]))^(2/3))/QuantityVariable["m", "Mass"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/570/5703fd37-934f-43a0-863f-8aee7669c15e/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Bose\[Dash]Einstein Condensation Temperature for Noninteracting \
Bosons Using Number Density"]]](images/570/5703fd37-934f-43a0-863f-8aee7669c15e-io-2-i.en.gif)
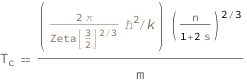
![FormulaData[
ResourceObject[
"Bose\[Dash]Einstein Condensation Temperature for Noninteracting \
Bosons Using Number Density"], {QuantityVariable[
"n","InverseVolume"] -> Quantity[1.5`*^10, 1/("Micrometers")^3],
QuantityVariable["s","Unitless"] -> 0}]](images/570/5703fd37-934f-43a0-863f-8aee7669c15e-io-3-i.en.gif)