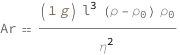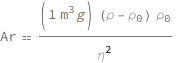Archimedes Number
The Archimedes number is used to determine the motion of fluids due to density differences. It is a dimensionless number defined as the ratio of external forces to internal viscous forces.
The Archimedes number equals the product of the cube of the characteristic length, the particle mass density, the difference in mass densities between the particle and the fluid and the local gravity divided by the square of the dynamic viscosity.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 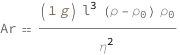 |
Use some values:
| Out[3]= | 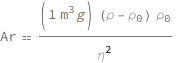 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Ar", "ArchimedesNumber"] == (Quantity[1, "StandardAccelerationOfGravity"]*QuantityVariable["l", "Length"]^3*(QuantityVariable["ρ", "MassDensity"] - QuantityVariable[Subscript["ρ", "0"], "MassDensity"])*QuantityVariable[Subscript["ρ", "0"], "MassDensity"])/QuantityVariable["η", "DynamicViscosity"]^2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/526/526793c8-0508-4b89-8161-4dc1d4485a17/Webpage/FormulaImage.png)