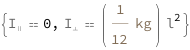Moment of Inertia of a Thin Rod
The parallel and perpendicular moments of inertia of a uniform, infinitely thin rod are taken through its center of mass. The rod is taken to be a one-dimensional wire. In the case of the perpendicular moment of inertia, the axis of rotation is at the midpoint of the rod. This is a special case of a thin rectangular plate with the axis of rotation at the center of the plate.
The parallel moment of inertia is zero. The perpendicular moment of inertia increases as the square of the length of the rod, and directly with the mass of the rod.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 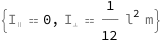 |
Use some values:
| Out[3]= | 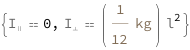 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["I", "∥"], "MomentOfInertia"] == 0, QuantityVariable[Subscript["I", "⊥"], "MomentOfInertia"] == (QuantityVariable["l", "Length"]^2*QuantityVariable["m", "Mass"])/12}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/51f/51f63213-81ae-48fb-8e71-1a09cafe1fb1/Webpage/FormulaImage.png)