Capacitance between Two Concentric Spheres
A capacitor is a passive, two-terminal electrical component that stores electrical energy in an electric field. In the case of two concentric spheres, the capacitance builds up between the inner surface of the outer sphere and the outer surface of the inner sphere.
The capacitance is proportional to the product of the inner and outer radii and the permittivity of the medium between them divided by the difference between the outer and inner radii of the spheres.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 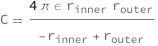 |
Use some values:
| Out[3]= | 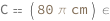 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["C", "ElectricCapacitance"] == (4*Pi*QuantityVariable["ε", "ElectricPermittivity"]*QuantityVariable[Subscript["r", "inner"], "Radius"]*QuantityVariable[Subscript["r", "outer"], "Radius"])/(-QuantityVariable[Subscript["r", "inner"], "Radius"] + QuantityVariable[Subscript["r", "outer"], "Radius"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/501/501b79ad-884e-4cdf-b68e-dbff7c65c000/Webpage/FormulaImage.png)
