Electric Field of Hollow Charged Sphere
The electric field of a hollow charged sphere describes a vector field that associates to each point in space the Coulomb force that would be experienced per unit of electric charge, by an infinitesimal test charge at that point.
The electric field of a hollow charged sphere depends on position, total charge and the radius of the sphere. Outside the sphere, it can be treated as a point charge decreasing with increasing distance. Inside the sphere, the electric potential is constant while the field strength is zero.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 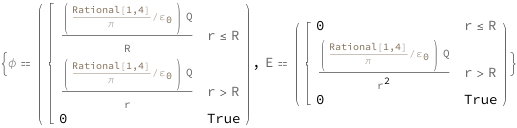 |
Use some values:
| Out[3]= | 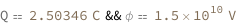 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["ϕ", "ElectricPotential"] == Piecewise[{{(Quantity[Rational[1, 4]/Pi, "ElectricConstant"^(-1)]*QuantityVariable["Q", "ElectricCharge"])/QuantityVariable["R", "Radius"], QuantityVariable["r", "Distance"] <= QuantityVariable["R", "Radius"]}, {(Quantity[Rational[1, 4]/Pi, "ElectricConstant"^(-1)]*QuantityVariable["Q", "ElectricCharge"])/QuantityVariable["r", "Distance"], QuantityVariable["r", "Distance"] > QuantityVariable["R", "Radius"]}}, 0], QuantityVariable["E", "ElectricFieldStrength"] == Piecewise[{{0, QuantityVariable["r", "Distance"] <= QuantityVariable["R", "Radius"]}, {(Quantity[Rational[1, 4]/Pi, "ElectricConstant"^(-1)]*QuantityVariable["Q", "ElectricCharge"])/QuantityVariable["r", "Distance"]^2, QuantityVariable["r", "Distance"] > QuantityVariable["R", "Radius"]}}, 0]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4ef/4ef5f833-a58f-435f-bf17-ff9c1c9809f7/Webpage/FormulaImage.png)


![FormulaData[
ResourceObject[
"Electric Field of Hollow Charged Sphere"], {QuantityVariable[
"E","ElectricFieldStrength"] ->
Quantity[10000000000, ("Volts")/("Meters")],
QuantityVariable["R","Radius"] -> Quantity[1, "Meters"],
QuantityVariable["r","Distance"] -> Quantity[1.5`, "Meters"]}]](images/4ef/4ef5f833-a58f-435f-bf17-ff9c1c9809f7-io-3-i.en.gif)