Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Minimum Variance Hedge Ratio

The hedge ratio compares the value of a position protected through the use of a hedge with the size of the entire position itself. The minimum variance hedge ratio is important when cross-hedging, which aims to minimize the variance of the position's value. The minimum variance hedge ratio, or optimal hedge ratio, is the product of the correlation coefficient between the changes in the spot and futures prices and the ratio of the standard deviation of the changes in the spot price to the standard deviation of the futures price.

The minimum variance hedge ratio equals the product of the correlation coefficient spot price change, futures price change and standard deviation spot price change divided by standard deviation futures price change.

Formula

QuantityVariable[SuperStar["h"], "Unitless"] == (QuantityVariable["ρ", "Unitless"]*QuantityVariable[Subscript["σ", "S"], "Money"])/QuantityVariable[Subscript["σ", "F"], "Money"]

symbol description physical quantity
h* minimum variance hedge ratio "Unitless"
ρ correlation coefficient spot price change futures price change "Unitless"
σF standard deviation futures price change "Money"
σS standard deviation spot price change "Money"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Minimum Variance Hedge Ratio"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Minimum Variance Hedge Ratio"]]
Out[2]=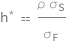

Use some values:

In[3]:=
FormulaData[ ResourceObject["Minimum Variance Hedge Ratio"], {QuantityVariable[ \!\(\*SubscriptBox[\("\[Sigma]"\), \("F"\)]\),"Money"] -> Quantity[2, "USDollars"], QuantityVariable[SuperStar["h"],"Unitless"] -> 0.5`, QuantityVariable[ \!\(\*SubscriptBox[\("\[Sigma]"\), \("S"\)]\),"Money"] -> Quantity[1, "USDollars"]}]
Out[3]=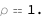

Publisher Information