Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Redlich–Kwong Equation of State

The Redlich–Kwong equation of state is an empirical, algebraic equation that relates temperature, pressure and volume of gases.

The pressure generally increases directly with temperature and Redlich-Kwong constant a. Increasing values of Redlich-Kwong constant b and volume tend to smaller values for pressure.

Formula

QuantityVariable["P", "Pressure"] == (Quantity[1, "MolarGasConstant"]*QuantityVariable["T", "Temperature"])/(-QuantityVariable["b", "RedlichKwongConstantB"] + QuantityVariable["V", "MolarVolume"]) - QuantityVariable["a", "RedlichKwongConstantA"]/(Sqrt[QuantityVariable["T", "Temperature"]]*QuantityVariable["V", "MolarVolume"]*(QuantityVariable["b", "RedlichKwongConstantB"] + QuantityVariable["V", "MolarVolume"]))

symbol description physical quantity
P pressure "Pressure"
T temperature "Temperature"
b Redlich–Kwong constant b "RedlichKwongConstantB"
V molar volume "MolarVolume"
a Redlich–Kwong constant a "RedlichKwongConstantA"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Redlich\[Dash]Kwong Equation of State"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Redlich\[Dash]Kwong Equation of State"]]
Out[2]=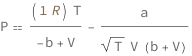

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Redlich\[Dash]Kwong Equation of State"], {QuantityVariable[ "P","Pressure"] -> Quantity[1, "Megapascals"], QuantityVariable["V","MolarVolume"] -> Quantity[0.0245`, ("Liters")/("Moles")], QuantityVariable["T","Temperature"] -> Quantity[298.15`, "Kelvins"], QuantityVariable["a","RedlichKwongConstantA"] -> Quantity[0.336`, (Sqrt["Kelvins"] ("Meters")^6 "Pascals")/( "Moles")^2]}]
Out[3]=

Source Metadata

  • Creator:
  • Date: 1949

Publisher Information