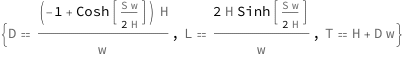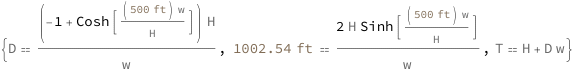Level Span Catenary Sag
The level span catenary sag describes the tensions and sagging curve, or catenary, of a cable connecting two points at the same elevation.
The sag increases with horizontal tension, and decreases with cable weight per unit length and span. The cable length increases with horizontal tension and span, and decreases with cable weight per unit length. The tension at the supports equals the horizontal tension plus the sag times the cable weight per unit length.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 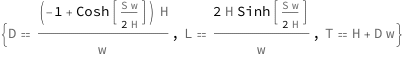 |
Use some values:
| Out[3]= | 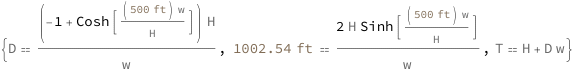 |
Publisher Information
![Copy to Clipboard {QuantityVariable["D", "Length"] == ((-1 + Cosh[(QuantityVariable["S", "Length"]*QuantityVariable["w", "ForceGradient"])/(2*QuantityVariable["H", "Force"])])*QuantityVariable["H", "Force"])/QuantityVariable["w", "ForceGradient"], QuantityVariable["L", "Length"] == (2*QuantityVariable["H", "Force"]*Sinh[(QuantityVariable["S", "Length"]*QuantityVariable["w", "ForceGradient"])/(2*QuantityVariable["H", "Force"])])/QuantityVariable["w", "ForceGradient"], QuantityVariable["T", "Force"] == QuantityVariable["H", "Force"] + QuantityVariable["D", "Length"]*QuantityVariable["w", "ForceGradient"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4d9/4d948130-1428-475c-bdec-3f032fd72889/Webpage/FormulaImage.png)