Elastic Collision in Two Dimensions Using Impact Parameter
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter. Perfectly elastic collisions occur only if there is no net conversion of kinetic energy into other forms.
The final speeds of two objects depend directly on the initial speed between the objects. The masses, the radii of the object and impact parameter also adjust this.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 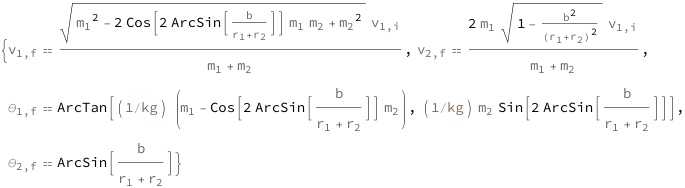 |
Use some values:
| Out[3]= | 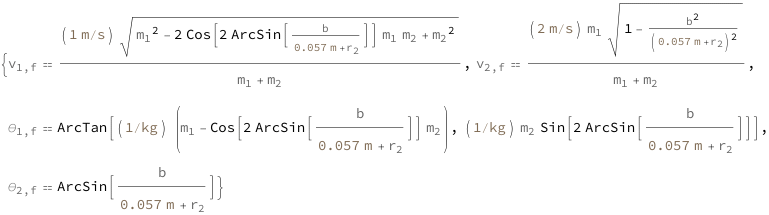 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["v", "1", "f"], "Speed"] == (Sqrt[QuantityVariable[Subscript["m", "1"], "Mass"]^2 - 2*Cos[2*ArcSin[QuantityVariable["b", "Length"]/(QuantityVariable[Subscript["r", "1"], "Radius"] + QuantityVariable[Subscript["r", "2"], "Radius"])]]*QuantityVariable[Subscript["m", "1"], "Mass"]*QuantityVariable[Subscript["m", "2"], "Mass"] + QuantityVariable[Subscript["m", "2"], "Mass"]^2]*QuantityVariable[Subscript["v", "1", "i"], "Speed"])/(QuantityVariable[Subscript["m", "1"], "Mass"] + QuantityVariable[Subscript["m", "2"], "Mass"]), QuantityVariable[Subscript["v", "2", "f"], "Speed"] == (2*QuantityVariable[Subscript["m", "1"], "Mass"]*Sqrt[1 - QuantityVariable["b", "Length"]^2/(QuantityVariable[Subscript["r", "1"], "Radius"] + QuantityVariable[Subscript["r", "2"], "Radius"])^2]*QuantityVariable[Subscript["v", "1", "i"], "Speed"])/(QuantityVariable[Subscript["m", "1"], "Mass"] + QuantityVariable[Subscript["m", "2"], "Mass"]), QuantityVariable[Subscript["θ", "1", "f"], "Angle"] == ArcTan[Quantity[1, "Kilograms"^(-1)]*(QuantityVariable[Subscript["m", "1"], "Mass"] - Cos[2*ArcSin[QuantityVariable["b", "Length"]/(QuantityVariable[Subscript["r", "1"], "Radius"] + QuantityVariable[Subscript["r", "2"], "Radius"])]]*QuantityVariable[Subscript["m", "2"], "Mass"]), Quantity[1, "Kilograms"^(-1)]*QuantityVariable[Subscript["m", "2"], "Mass"]*Sin[2*ArcSin[QuantityVariable["b", "Length"]/(QuantityVariable[Subscript["r", "1"], "Radius"] + QuantityVariable[Subscript["r", "2"], "Radius"])]]], QuantityVariable[Subscript["θ", "2", "f"], "Angle"] == ArcSin[QuantityVariable["b", "Length"]/(QuantityVariable[Subscript["r", "1"], "Radius"] + QuantityVariable[Subscript["r", "2"], "Radius"])]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4cc/4ccc5ec4-bd05-4de6-adc2-52717ae87fba/Webpage/FormulaImage.png)

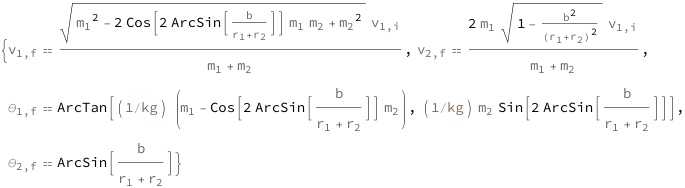
![FormulaData[
ResourceObject[
"Elastic Collision in Two Dimensions Using Impact Parameter"], \
{QuantityVariable[
\!\(\*SubscriptBox[\("v"\), \("1", "i"\)]\),"Speed"] ->
Quantity[1, ("Meters")/("Seconds")], QuantityVariable[
\!\(\*SubscriptBox[\("r"\), \("1"\)]\),"Radius"] ->
Quantity[0.057`, "Meters"]}]](images/4cc/4ccc5ec4-bd05-4de6-adc2-52717ae87fba-io-3-i.en.gif)