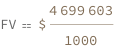Future Value of Annuity
An annuity is a series of payments made at equal intervals. The future value of an annuity is the accumulated amount, including payments and interest, of a stream of payments made to an interest-bearing account.
The future value of an annuity depends on the value of periodic payments multiplied by the interest compounded over the number of periods, accounting for the frequency of payments and any growth in the periodic payments.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 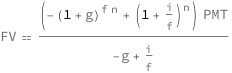 |
Use some values:
| Out[3]= | 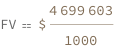 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["FV", "Money"] == ((-(1 + QuantityVariable["g", "Unitless"])^(QuantityVariable["f", "Unitless"]*QuantityVariable["n", "Unitless"]) + (1 + QuantityVariable["i", "Unitless"]/QuantityVariable["f", "Unitless"])^QuantityVariable["n", "Unitless"])*QuantityVariable["PMT", "Money"])/(-QuantityVariable["g", "Unitless"] + QuantityVariable["i", "Unitless"]/QuantityVariable["f", "Unitless"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4b8/4b8f2e62-754b-4955-a9c8-ac009fd8c0f3/Webpage/FormulaImage.png)

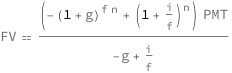
![FormulaData[
ResourceObject[
"Future Value of Annuity"], {QuantityVariable["i","Unitless"] ->
Quantity[8, "Percent"], QuantityVariable["f","Unitless"] -> 1,
QuantityVariable["PMT","Money"] -> Quantity[1000, "USDollars"],
QuantityVariable["n","Unitless"] -> 4,
QuantityVariable["g","Unitless"] -> Quantity[3, "Percent"]}]](images/4b8/4b8f2e62-754b-4955-a9c8-ac009fd8c0f3-io-3-i.en.gif)