Bodenstein Number with Thermal Conductivity
The Bodenstein number, a dimensionless number that is often used to describe axial mixing in so-called axial-dispersion models for tubular reactors. It represents the ratio between the convective transport to the transport by axial diffusion.
The Bodenstein number equals the thermal conductivity divided by the product of the specific heat capacity, characteristic length, characteristic speed and the mass density.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 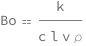 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Bo", "BodensteinNumber"] == QuantityVariable["k", "ThermalConductivity"]/(QuantityVariable["c", "SpecificHeatCapacity"]*QuantityVariable["l", "Length"]*QuantityVariable["v", "Speed"]*QuantityVariable["ρ", "MassDensity"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4b1/4b175708-5271-4556-84f3-5a789669e8c8/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Bodenstein Number with Thermal Conductivity"], {QuantityVariable[
"\[Rho]","MassDensity"] ->
Quantity[1000, ("Kilograms")/("Meters")^3],
QuantityVariable["Bo","BodensteinNumber"] -> 1,
QuantityVariable["k","ThermalConductivity"] ->
Quantity[1, ("Watts")/("KelvinsDifference" "Meters")],
QuantityVariable["l","Length"] -> Quantity[1, "Meters"],
QuantityVariable["v","Speed"] ->
Quantity[1, ("Meters")/("Seconds")]}]](images/4b1/4b175708-5271-4556-84f3-5a789669e8c8-io-3-i.en.gif)
