Normalized Frequency
The normalized frequency, or V number, is a parameter used in optical fibers.
The normalized frequency is proportional to the radius of the fiber divided by the wavelength times the square root of the difference of the squares of the maximum refractive index of the core and the refractive index of the homogeneous cladding.
Formula
![QuantityVariable["V", "NormalizedFrequency"] == (2*Pi*QuantityVariable["R", "Radius"]*Sqrt[QuantityVariable[Subscript["n", "1"], "RefractiveIndex"]^2 - QuantityVariable[Subscript["n", "2"], "RefractiveIndex"]^2])/QuantityVariable["λ", "Wavelength"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4ab/4abf97d1-fb40-4dfd-9eb7-8c07108d70f2/Webpage/FormulaImage.png "Copy to Clipboard")
| symbol | description | physical quantity |
|---|---|---|
| V | normalized frequency | "NormalizedFrequency" |
| R | radius | "Radius" |
| λ | wavelength | "Wavelength" |
| n1 | maximum refractive index of the core | "RefractiveIndex" |
| n2 | refractive index of the homogeneous cladding | "RefractiveIndex" |
Forms
Examples
Get the resource:
| In[1]:= | ![ResourceObject["Normalized Frequency"]](images/4ab/4abf97d1-fb40-4dfd-9eb7-8c07108d70f2-io-1-i.en.gif){kind=small} |
| Out[1]= |  |
Get the formula:
| In[2]:= | ![FormulaData[ResourceObject["Normalized Frequency"]]](images/4ab/4abf97d1-fb40-4dfd-9eb7-8c07108d70f2-io-2-i.en.gif){kind=small} |
| Out[2]= |  |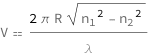
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject["Normalized Frequency"], {QuantityVariable[
\!\(\*SubscriptBox[\("n"\), \("1"\)]\),"RefractiveIndex"] -> 1.33`,
QuantityVariable["\[Lambda]","Wavelength"] ->
Quantity[450, "Nanometers"]}]](images/4ab/4abf97d1-fb40-4dfd-9eb7-8c07108d70f2-io-3-i.en.gif){kind=small} |
| Out[3]= | 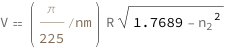 |