Grashof Number
The Grashof number is a dimensionless number in fluid dynamics and heat transfer that approximates the ratio of the buoyancy to viscous force acting on a fluid.
The Grashof number equals the product of the characteristic length cubed, the coefficient of thermal expansion, the temperature difference and the acceleration of gravity divided by the kinematic viscosity squared.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 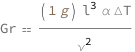 |
Use some values:
| Out[3]= | 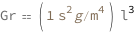 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Gr", "GrashofNumberHeatTransfer"] == (Quantity[1, "StandardAccelerationOfGravity"]*QuantityVariable["l", "Length"]^3*QuantityVariable["α", "ThermalExpansionCoefficient"]*QuantityVariable["ΔT", "TemperatureDifference"])/QuantityVariable["ν", "KinematicViscosity"]^2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4a7/4a780d06-9ab7-4165-8215-688354b44939/Webpage/FormulaImage.png)