Wave Propagation in Strings
The velocity of propagation of a wave in a string is proportional to the square root of the force of tension of the string, and inversely proportional to the square root of the linear density of the string.
The wave propagation speed equals the square root of the string tension divided by the linear mass density.
Formula
![Copy to Clipboard QuantityVariable["v", "Speed"] == Sqrt[QuantityVariable["T", "Tension"]/QuantityVariable["μ", "LinearMassDensity"]]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/4a4/4a4aec20-6f4b-417f-ab9c-fdc842978ad4/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| v | wave propagation speed | "Speed" |
| T | string tension | "Tension" |
| μ | linear mass density | "LinearMassDensity" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 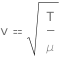 |
Use some values:
| In[3]:= |
| Out[3]= | 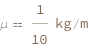 |