Diesel Cycle
The Diesel cycle is a combustion process of a reciprocating internal combustion engine. In it, fuel is ignited by heat generated during the compression of air in the combustion chamber, into which fuel is then injected.
The thermal efficiency depends on compression ratio, hot and cold reservoir temperatures and the heat capacity ratio.
Formula
![Copy to Clipboard QuantityVariable[Subscript["η", "th"], "ThermalEfficiency"] == 1 - (QuantityVariable["r", "Unitless"]*QuantityVariable[Subscript["T", "c"], "Temperature"]*(1 - ((QuantityVariable["r", "Unitless"]^(1 - QuantityVariable["γ", "HeatCapacityRatio"])*QuantityVariable[Subscript["T", "h"], "Temperature"])/QuantityVariable[Subscript["T", "c"], "Temperature"])^QuantityVariable["γ", "HeatCapacityRatio"]))/(QuantityVariable["γ", "HeatCapacityRatio"]*(QuantityVariable["r", "Unitless"]^QuantityVariable["γ", "HeatCapacityRatio"]*QuantityVariable[Subscript["T", "c"], "Temperature"] - QuantityVariable["r", "Unitless"]*QuantityVariable[Subscript["T", "h"], "Temperature"]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/484/4840e7a4-d365-41b4-8f86-30e82d39d7a4/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| ηth | thermal efficiency | "ThermalEfficiency" |
| r | compression ratio | "Unitless" |
| γ | heat capacity ratio | "HeatCapacityRatio" |
| Tc | cold reservoir temperature | "Temperature" |
| Th | hot reservoir temperature | "Temperature" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 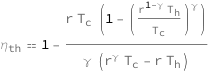 |
Use some values:
| In[3]:= |
| Out[3]= | 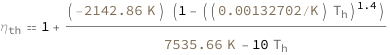 |