Spherical Law of Cosines Using Angles
The spherical law of cosines is a theorem relating the sides and angles of spherical triangles, analogous to the ordinary law of cosines from plane trigonometry.
The cosine of the angle opposite the third side equals the product of the cosine of the angular length of the third side and the sines of the angles opposite the first and second sides minus the product of the cosines of the angles opposite the first and second sides.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 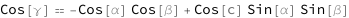 |
Use some values:
| Out[3]= | 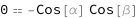 |
External Links
Publisher Information
![Copy to Clipboard Cos[QuantityVariable["γ", "Angle"]] == -(Cos[QuantityVariable["α", "Angle"]]*Cos[QuantityVariable["β", "Angle"]]) + Cos[QuantityVariable["c", "Angle"]]*Sin[QuantityVariable["α", "Angle"]]*Sin[QuantityVariable["β", "Angle"]]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/478/47800816-66f5-4800-a858-79d25fda9596/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Spherical Law of Cosines Using Angles"], {QuantityVariable[
"c","Angle"] -> Quantity[\[Pi]/2, "Radians"],
QuantityVariable["\[Gamma]","Angle"] ->
Quantity[\[Pi]/2, "Radians"]}]](images/478/47800816-66f5-4800-a858-79d25fda9596-io-3-i.en.gif)