Weber Number
The Weber number is a dimensionless number in fluid mechanics that is often useful in analyzing fluid flows where there is an interface between two different fluids, especially for multiphase flows with strongly curved surfaces.
The Weber number equals the product of the characteristic length, characteristic speed squared and the mass density divided by the surface tension.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 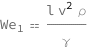 |
Use some values:
| Out[3]= | 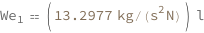 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["We", "1"], "WeberNumber1"] == (QuantityVariable["l", "Length"]*QuantityVariable["v", "Speed"]^2*QuantityVariable["ρ", "MassDensity"])/QuantityVariable["γ", "SurfaceTension"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/465/4654295f-08de-4a47-97d5-6c7ff963d8f4/Webpage/FormulaImage.png)

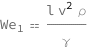
![FormulaData[ResourceObject["Weber Number"], {QuantityVariable[
\!\(\*SubscriptBox[\("We"\), \("1"\)]\),"WeberNumber1"] -> 2.39`,
QuantityVariable["\[Gamma]","SurfaceTension"] ->
Quantity[75.2007`, ("Newtons")/("Meters")],
QuantityVariable["v","Speed"] ->
Quantity[1, ("Meters")/("Seconds")],
QuantityVariable["\[Rho]","MassDensity"] ->
Quantity[1000, ("Kilograms")/("Meters")^3]}]](images/465/4654295f-08de-4a47-97d5-6c7ff963d8f4-io-3-i.en.gif)