Expected Fielding Independent Pitching
Expected fielding independent pitching is a measurement of a pitcher's performance that controls for the quality of his team's defense.
The expected fielding independent pitching increases with the number of walks and flyballs, and decreases with the number of strikeouts. It also declines with the relative number of innings played and outs recorded.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= |  |
Use some values:
| Out[3]= | 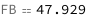 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["xFIP", "Unitless"] == 3.1 + (3*QuantityVariable["BB", "Unitless"] + 1.3519999999999999*QuantityVariable["FB", "Unitless"] - 2*QuantityVariable["K", "Unitless"])/(QuantityVariable["IP", "Unitless"] + QuantityVariable["OUTS", "Unitless"]/3)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/43a/43a3f3c8-022e-40e7-ae3c-10b09959f4ff/Webpage/FormulaImage.png)

