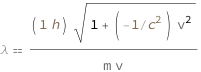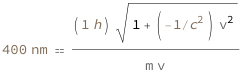Relativistic de Broglie Wavelength by Velocity
The de Broglie wavelength is the wavelength associated with a massive particle in motion according to quantum mechanics, accounting for relativistic effects.
The de Broglie wavelength is proportional to the square root of the difference between 1 and the square of the ratio between the velocity and the speed of light. This is then divided by the mass times velocity.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 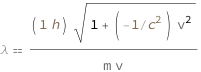 |
Use some values:
| Out[3]= | 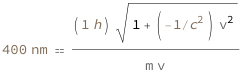 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["λ", "Wavelength"] == (Quantity[1, "PlanckConstant"]*Sqrt[1 + Quantity[-1, "SpeedOfLight"^(-2)]*QuantityVariable["v", "Speed"]^2])/(QuantityVariable["m", "Mass"]*QuantityVariable["v", "Speed"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/435/435fca03-fd8a-4037-b3fa-4a681c903f93/Webpage/FormulaImage.png)