Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Thermal de Broglie Wavelength for Massive Particles

The thermal de Broglie wavelength is roughly the average de Broglie wavelength of the gas particles in an ideal gas at the specified temperature.

The thermal de Broglie wavelength is proportional to the reciprocal of the square root of the product of the temperature and mass of a particle.

Formula

QuantityVariable["Λ", "Wavelength"] == Quantity[1/Sqrt[2*Pi], "PlanckConstant"]/Sqrt[Quantity[1, "BoltzmannConstant"]*QuantityVariable["m", "Mass"]*QuantityVariable["T", "Temperature"]]

symbol description physical quantity
Λ thermal de Broglie wavelength "Wavelength"
m mass of a particle "Mass"
T temperature "Temperature"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Thermal de Broglie Wavelength for Massive Particles"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ ResourceObject[ "Thermal de Broglie Wavelength for Massive Particles"]]
Out[2]=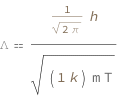

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Thermal de Broglie Wavelength for Massive Particles"], \ {QuantityVariable["T","Temperature"] -> Quantity[273.15`, "Kelvins"], QuantityVariable["\[CapitalLambda]","Wavelength"] -> Quantity[0.1`, "Nanometers"]}]
Out[3]=

Source Metadata

  • Contributor:

Publisher Information