Weighted Average Cost of Capital
The weighted average cost of capital is the rate that a company is expected to pay on average to all its security holders to finance its assets.
The weighted average cost of capital equals the sum of the product of the total debt, 1 minus the tax rate, and the cost of debt and total equity times the cost of equity divided by the sum of the total debt and total equity.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 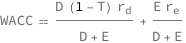 |
Use some values:
| Out[3]= | 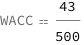 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["WACC", "Unitless"] == (QuantityVariable["D", "Money"]*(1 - QuantityVariable["T", "Unitless"])*QuantityVariable[Subscript["r", "d"], "Unitless"])/(QuantityVariable["D", "Money"] + QuantityVariable["E", "Money"]) + (QuantityVariable["E", "Money"]*QuantityVariable[Subscript["r", "e"], "Unitless"])/(QuantityVariable["D", "Money"] + QuantityVariable["E", "Money"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/42b/42b66232-7f21-44de-af26-917589daf55d/Webpage/FormulaImage.png)
![FormulaData[
ResourceObject["Weighted Average Cost of Capital"], {QuantityVariable[
\!\(\*SubscriptBox[\("r"\), \("e"\)]\),"Unitless"] ->
Quantity[12, "Percent"],
QuantityVariable["T","Unitless"] -> Quantity[35, "Percent"],
QuantityVariable["D","Money"] -> Quantity[1000, "USDollars"],
QuantityVariable[
\!\(\*SubscriptBox[\("r"\), \("d"\)]\),"Unitless"] ->
Quantity[8, "Percent"],
QuantityVariable["E","Money"] -> Quantity[1000, "USDollars"]}]](images/42b/42b66232-7f21-44de-af26-917589daf55d-io-3-i.en.gif)