Lorentz Number
The Lorentz number is a dimensionless number that relates the thermal conductivity of a metal to its temperature and its electrical conductivity.
The Lorentz number equals voltage squared times specific electrical conductivity divided by the temperature difference and specific thermal conductivity.
Formula
![Copy to Clipboard QuantityVariable["γ", "RelativisticGamma"] == (QuantityVariable["V", "ElectricPotential"]^2*QuantityVariable["σ", "ElectricConductivity"])/(QuantityVariable["ΔT", "TemperatureDifference"]*QuantityVariable["λ", "ThermalConductivity"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/42a/42a46ebd-15ea-4bf2-9bec-72455c2ba35b/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| γ | Lorentz number | "RelativisticGamma" |
| V | voltage | "ElectricPotential" |
| ΔT | temperature difference | "TemperatureDifference" |
| λ | specific thermal conductivity | "ThermalConductivity" |
| σ | specific electrical conductivity | "ElectricConductivity" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |
Use some values:
| In[3]:= |
| Out[3]= | 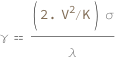 |