Natural Broadening
The uncertainty principle relates the lifetime of an excited state (due to spontaneous radiative decay or the Auger process) with the uncertainty of its energy. A short lifetime will have a large energy uncertainty and a broad emission. This broadening effect results in an unshifted Lorentzian profile. The natural broadening can be experimentally altered only to the extent that decay rates can be artificially suppressed or enhanced.
The frequency full width at half-maximum equals the reciprocal of twice the excited state lifetime.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 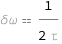 |
Use some values:
| Out[3]= | 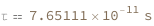 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["δ ω", "Frequency"] == 1/(2*QuantityVariable["τ", "Lifetime"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/417/417dda13-7824-4e46-966f-00aff497b1d4/Webpage/FormulaImage.png)
