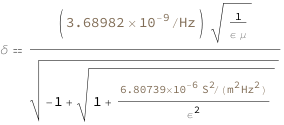Electromagnetic Skin Depth
Skin depth is a property of the skin effect, the tendency of an alternating electric current (AC) to become distributed within a conductor such that the current density is largest near the surface of the conductor, and decreases with greater depths in the conductor. The electric current flows mainly at the skin of the conductor, between the outer surface and a level called the skin depth.
Skin depth increases inversely with decreasing electric conductivity and magnetic permeability. Increasing electric permittivity also leads to a larger skin depth. The effect of frequency is more complicated, but for high frequencies, skin depth is roughly proportional to the reciprocal of the square root of the frequency.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 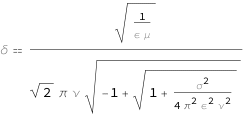 |
Use some values:
| Out[3]= | 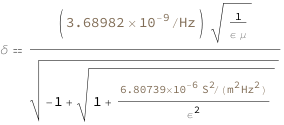 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["δ", "Depth"] == Sqrt[1/(QuantityVariable["ε", "ElectricPermittivity"]*QuantityVariable["μ", "MagneticPermeability"])]/(Sqrt[2]*Pi*QuantityVariable["ν", "Frequency"]*Sqrt[-1 + Sqrt[1 + QuantityVariable["σ", "ElectricConductivity"]^2/(4*Pi^2*QuantityVariable["ε", "ElectricPermittivity"]^2*QuantityVariable["ν", "Frequency"]^2)]])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/3b2/3b25c054-5b86-44b3-8386-336102f61598/Webpage/FormulaImage.png)