Field of View
The field of view is the portion of the focused subject visible through the camera lens, assuming a rectilinear lens.
The vertical field of view equals the height of the image format divided by the subject magnification factor. The subject magnification factor equals the focal length divided by the subject distance minus the focal length.
Formula
![Copy to Clipboard {QuantityVariable[Subscript["V", "v"], "Height"] == QuantityVariable["h", "Height"]/QuantityVariable["M", "Unitless"], QuantityVariable["M", "Unitless"] == QuantityVariable["f", "Length"]/(-QuantityVariable["f", "Length"] + QuantityVariable["s", "Length"])}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/37b/37b379c9-a1e8-4127-bf91-93cdce38fbc0/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| Vv | vertical field of view | "Height" |
| h | height of image format | "Height" |
| M | subject magnification factor | "Unitless" |
| f | focal length | "Length" |
| s | subject distance | "Length" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |
Use some values:
| In[3]:= |
| Out[3]= | 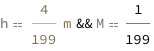 |