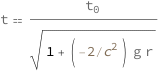Gravitational Time Dilation Using Gravity
Gravitational time dilation is a form of time dilation, an actual difference of elapsed time between two events as measured by observers situated at varying distances from a gravitating mass. The higher the gravitational potential (the farther the clock is from the source of gravitation), the faster time passes.
The time seen by a stationary observer equals the time in rest frame divided by the square root of 1 minus twice the ratio of the gravitational acceleration times the radius from the center of the massive object to the speed of light squared.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 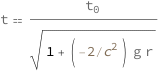 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["t", "Time"] == QuantityVariable[Subscript["t", "0"], "Time"]/Sqrt[1 + Quantity[-2, "SpeedOfLight"^(-2)]*QuantityVariable["g", "GravitationalAcceleration"]*QuantityVariable["r", "Radius"]]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/35f/35f2ec29-9bce-4399-8e6f-ffbf3fa7b82f/Webpage/FormulaImage.png)