Doyle's Log Rule
Doyle's log rule describes the volume of wood in a standing tree or log.
The volume of wood is proportional to the diameter minus 4 inches squared times the length of the log.
Formula
![Copy to Clipboard QuantityVariable["V", "Volume"] == Quantity[1/16, "BoardFeet"/"Feet"]*(-4 + Quantity[1, "Inches"^(-1)]*QuantityVariable["d", "Diameter"])^2*QuantityVariable["L", "Length"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/35c/35c509dd-9332-49da-9d6c-8d48e4c6e483/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| V | volume | "Volume" |
| d | diameter | "Diameter" |
| L | length | "Length" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 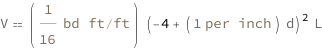 |
Use some values:
| In[3]:= |
| Out[3]= | 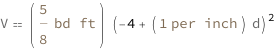 |