Macaulay Duration of Bonds
Modified duration is the name given to the weighted average time until cash flows are received, and is measured in years.
The Macaulay duration depends on a nonlinear combination of coupon frequency, the number of whole coupon periods, the fraction of year until next coupon, annual yield and the annual coupon rate.
Formula
![Copy to Clipboard QuantityVariable["D", "Unitless"]*QuantityVariable["f", "Unitless"] == (-QuantityVariable["y", "Unitless"]^2 + QuantityVariable["n", "Unitless"]*QuantityVariable["y", "Unitless"]*(QuantityVariable["y", "Unitless"] - QuantityVariable[Subscript["r", "c"], "Unitless"]) - QuantityVariable["f", "Unitless"]*QuantityVariable[Subscript["r", "c"], "Unitless"] + QuantityVariable["f", "Unitless"]*((QuantityVariable["f", "Unitless"] + QuantityVariable["y", "Unitless"])/QuantityVariable["f", "Unitless"])^QuantityVariable["n", "Unitless"]*QuantityVariable[Subscript["r", "c"], "Unitless"] + QuantityVariable["y", "Unitless"]*QuantityVariable["α", "Unitless"]*(QuantityVariable["y", "Unitless"] + (-1 + ((QuantityVariable["f", "Unitless"] + QuantityVariable["y", "Unitless"])/QuantityVariable["f", "Unitless"])^QuantityVariable["n", "Unitless"])*QuantityVariable[Subscript["r", "c"], "Unitless"]))/(QuantityVariable["y", "Unitless"]*(QuantityVariable["y", "Unitless"] + (-1 + ((QuantityVariable["f", "Unitless"] + QuantityVariable["y", "Unitless"])/QuantityVariable["f", "Unitless"])^QuantityVariable["n", "Unitless"])*QuantityVariable[Subscript["r", "c"], "Unitless"]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/345/3455fdda-2ca3-4f43-b473-123fdc4a8d73/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| D | duration | "Unitless" |
| f | coupon frequency | "Unitless" |
| y | annual yield | "Unitless" |
| n | number of whole coupon periods | "Unitless" |
| rc | annual coupon rate | "Unitless" |
| α | fraction of year until next coupon | "Unitless" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 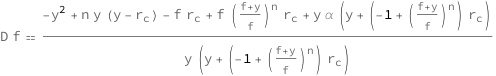 |
Use some values:
| In[3]:= |
| Out[3]= | 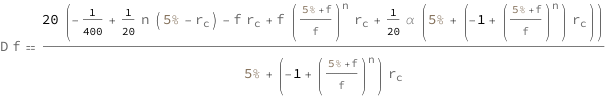 |