Pendulum Harmonic Oscillator
A pendulum harmonic oscillator is a pendulum that, when displaced from its equilibrium position, experiences a restoring force proportional to the displacement.
The angular frequency for a pendulum harmonic oscillator equals the natural angular frequency. It is also equal to 2\[Pi] times the frequency. The frequency equals the reciprocal of the period. The natural angular frequency equals the square root of the ratio of the acceleration due to gravity and the length of the pendulum.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 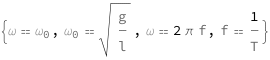 |
Use some values:
| Out[3]= | 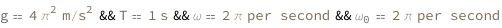 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["ω", "AngularFrequency"] == QuantityVariable[Subscript["ω", "0"], "AngularFrequency"], QuantityVariable[Subscript["ω", "0"], "AngularFrequency"] == Sqrt[QuantityVariable["g", "GravitationalAcceleration"]/QuantityVariable["l", "Length"]], QuantityVariable["ω", "AngularFrequency"] == 2*Pi*QuantityVariable["f", "Frequency"], QuantityVariable["f", "Frequency"] == QuantityVariable["T", "Period"]^(-1)}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/340/34001d2c-8b51-4fec-9b79-ea2931a9bd67/Webpage/FormulaImage.png)