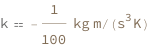Fourier's Law
The law of heat conduction, also known as Fourier's law, states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area, at right angles to that gradient, through which the heat flows.
The heat flux equals the negative of the product of the thermal conductivity and the difference between the equilibrium temperature and the current temperature divided by the distance.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 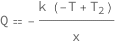 |
Use some values:
| Out[3]= | 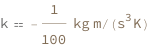 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Q", "HeatFlux"] == -((QuantityVariable["k", "ThermalConductivity"]*(-QuantityVariable["T", "Temperature"] + QuantityVariable[Subscript["T", "2"], "Temperature"]))/QuantityVariable["x", "Distance"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/322/322dbe33-20b6-4194-b187-5d446913e752/Webpage/FormulaImage.png)