Rectangular Resonant Cavity Using Conductivity
A microwave cavity or radio frequency (RF) cavity is a special type of resonator consisting of a closed (or largely closed) metal structure that confines electromagnetic fields in the microwave region of the spectrum. The structure is either hollow or filled with dielectric material. The microwaves bounce back and forth between the walls of the cavity. At the cavity's resonant frequencies, they reinforce to form standing waves in the cavity.
The resonant frequency is proportional to the square root of the sum of the squares of the ratios of the modes and the side lengths. The wavelength is proportional to the reciprocal of the square root of the sum of the squares of the ratios of the modes and the side lengths. The electromagnetic skin resistance equals the reciprocal of the conductor conductivity times the electromagnetic skin depth. The electromagnetic skin depth is proportional to the reciprocal of the square root of the conductor conductivity times the frequency.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 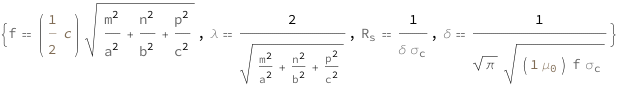 |
Use some values:
| Out[3]= | 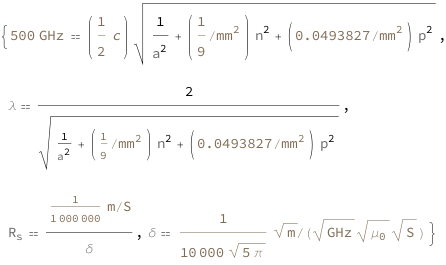 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["f", "Frequency"] == Quantity[1/2, "SpeedOfLight"]*Sqrt[QuantityVariable["m", "Unitless"]^2/QuantityVariable["a", "Length"]^2 + QuantityVariable["n", "Unitless"]^2/QuantityVariable["b", "Length"]^2 + QuantityVariable["p", "Unitless"]^2/QuantityVariable["c", "Length"]^2], QuantityVariable["λ", "Wavelength"] == 2/Sqrt[QuantityVariable["m", "Unitless"]^2/QuantityVariable["a", "Length"]^2 + QuantityVariable["n", "Unitless"]^2/QuantityVariable["b", "Length"]^2 + QuantityVariable["p", "Unitless"]^2/QuantityVariable["c", "Length"]^2], QuantityVariable[Subscript["R", "s"], "ElectricResistance"] == 1/(QuantityVariable["δ", "Depth"]*QuantityVariable[Subscript["σ", "c"], "ElectricConductivity"]), QuantityVariable["δ", "Depth"] == 1/(Sqrt[Pi]*Sqrt[Quantity[1, "MagneticConstant"]*QuantityVariable["f", "Frequency"]*QuantityVariable[Subscript["σ", "c"], "ElectricConductivity"]])}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/315/315973ce-8718-4e49-8f8f-5a08f3655514/Webpage/FormulaImage.png)

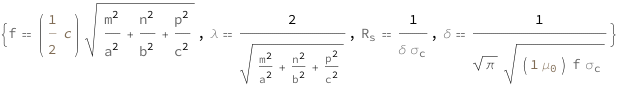
![FormulaData[
ResourceObject[
"Rectangular Resonant Cavity Using Conductivity"], \
{QuantityVariable["b","Length"] -> Quantity[3, "Millimeters"],
QuantityVariable["f","Frequency"] -> Quantity[500, "Gigahertz"],
QuantityVariable[
\!\(\*SubscriptBox[\("\[Sigma]"\), \("c"\)]\),
"ElectricConductivity"] ->
Quantity[1000000, ("Siemens")/("Meters")],
QuantityVariable["m","Unitless"] -> 1,
QuantityVariable["c","Length"] -> Quantity[4.5`, "Millimeters"]}]](images/315/315973ce-8718-4e49-8f8f-5a08f3655514-io-3-i.en.gif)